Computational Optimization, Design and Control
The unifying feature of engineering and scientific design is the presence of an underlying optimization problem. This problem is not always explicit, and design strategies are sometimes formulated on an ad-hoc basis, without formal reference to the underlying optimization problem. One of the goals of the research in this field of the School for Computational Science and Engineering is to integrate the insight offered by formal computational optimization methods into the development of design techniques in areas as diverse as the control of chemical reactions, computational flow control, signal processing and communication systems. Concurrently, the application of computational optimization methods in these application areas will expose the limitations of currently available algorithms and implementations. It will stimulate the development of new algorithms for classes of problems that designers would like to solve, and development of improved algorithms and implementations for problems for which existing tools do not satisfy the designers’ requirements.
In recent years, McMaster has development nodes of expertise in the following areas:
- Computational optimization (Dr. Deza, Canada Research Chair)
- Inverse problems in fluid mechanics (Dr. Protas, SHARCNET Chair, Early Researcher Award recipient)
- Computational design and applications in control (Dr. Swartz)
- Signal processing and communications (Dr. Davidson, Canada Research Chair)
- Nuclear Safety Analysis Computational Methods (Dr. Luxat, NSERC/UNENE Industrial Research Chair)
- Optimization in finance (Dr. Grasselli, SHARCNET Chair) and business (Dr. Hassini).
The field of Computational Optimization, Design and Control will solidify the emerging, but fragmented, interactions between these nodes of expertise, and will provide substantial opportunities for graduate students to make lasting contributions.
Information Box Group

Computational Geometry
Hamiltonian circuit on the dual 4-chamfered cube
(Antoine Deza)
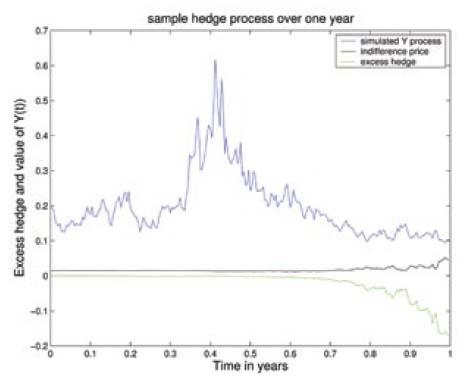
Optimization in Finance
Indifference price and excess hedge for a volatility put option
(Tamás Terlaky)

Image Analysis
Surface reconstruction from a structured light image
(Tamás Terlaky)

